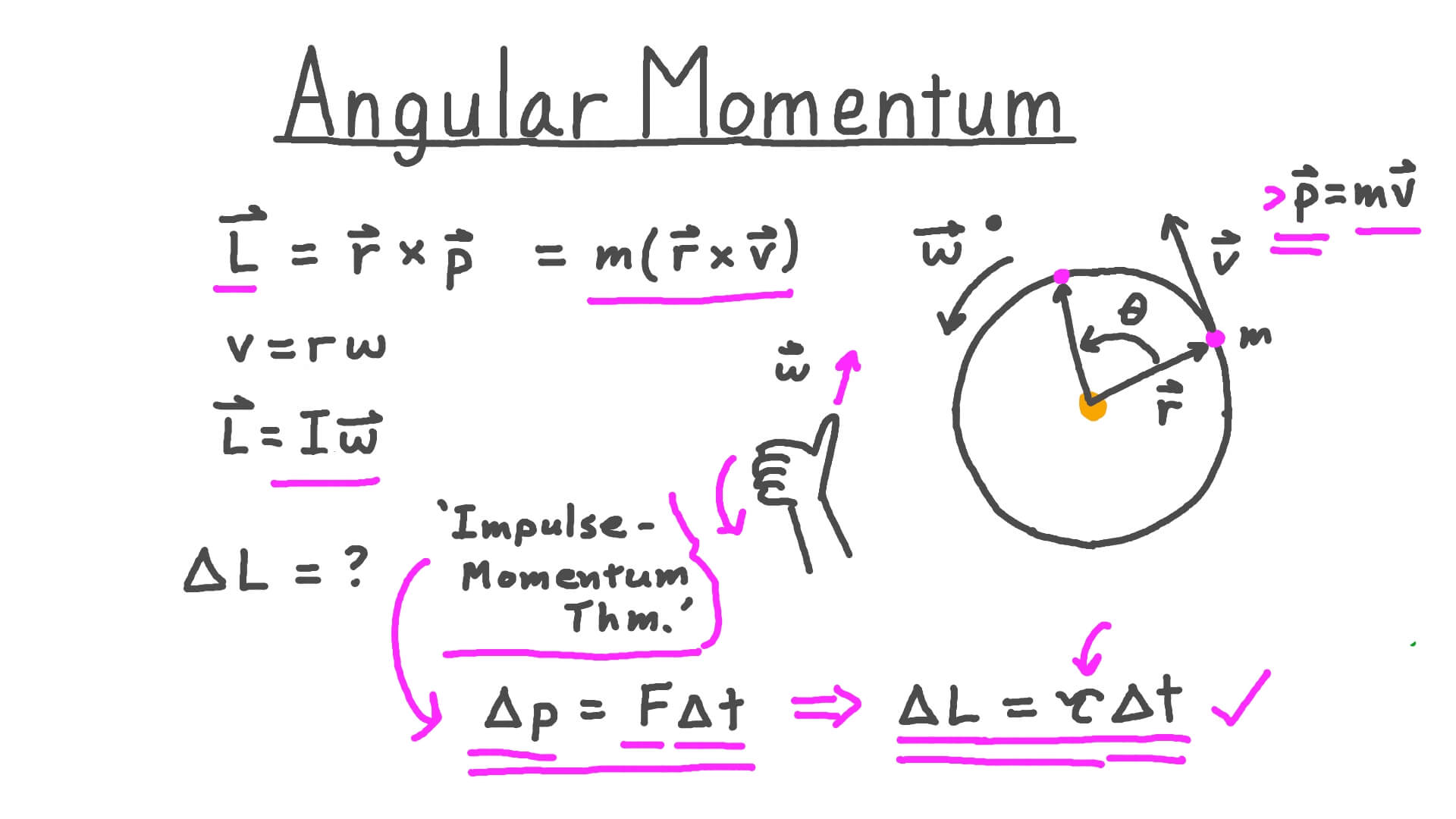
Angular momentum is a fundamental concept in physics that describes the rotational motion of an object. In classical mechanics, angular momentum (often denoted as L) is defined as the cross product of the position vector (r) and the linear momentum (p) of an object:

L = r × p

Conservation of Angular Momentum:

 In the absence of external torques, the total angular momentum of a system remains constant. This is analogous to the conservation of linear momentum.

Angular Velocity:

 Angular momentum depends on the angular velocity (ω) of an object. Higher angular velocity results in greater angular momentum.

Direction of Angular Momentum:

 The direction of angular momentum is perpendicular to both the direction of the position vector (r) and the direction of linear momentum (p).

Units: The SI unit of angular momentum is kilogram meters squared per second (kg·m²/s).

Torque:

 A torque applied to an object can change its angular momentum. Torque is the rotational analog of force.

Moment of Inertia: The moment of inertia (I) of an object quantifies how the mass is distributed around the axis of rotation. It affects the angular momentum of an object.

Right-Hand Rule: The direction of angular momentum is determined using the right-hand rule. If you curl your fingers from r to p, your thumb points in the direction of angular momentum.

Angular Momentum of a Point Particle: For a point particle with mass m, angular momentum is given by L = r × (m * v), where v is the linear velocity.

Rotational Kinetic Energy: Angular momentum is related to the rotational kinetic energy (K) of an object. K = 1/2 * I * ω².

Conservation of Angular Momentum in Orbits: Planets and satellites conserve angular momentum as they move in elliptical orbits around the Sun. When they're closer to the Sun, they move faster to maintain this conservation.

Gyroscopic Precession: Gyroscopes exhibit precession due to the conservation of angular momentum. This behavior is used in navigation and stability applications.

Angular Momentum in Quantum Mechanics:

 In quantum mechanics, angular momentum is quantized. The eigenvalues of angular momentum operators are quantized, and angular momentum is a fundamental property of subatomic particles.

Spin Angular Momentum:

 Elementary particles, such as electrons and quarks, have intrinsic angular momentum called spin. It is a quantum property and is not due to actual spinning.

Angular Momentum in Rigid Bodies:

 In rigid bodies, angular momentum is the sum of the angular momenta of its individual particles, which can be calculated as the integral of r × p over the entire body.

Conservation of Angular Momentum in Collisions:

 In collisions or interactions, the total angular momentum before the event is equal to the total angular momentum after the event if no external torques are present.

Applications: Angular momentum is crucial in various real-world applications, including the behavior of spinning tops, the motion of wheels and flywheels, the stability of satellites, and the operation of engines.

Understanding angular momentum is essential in classical and quantum physics, and it has numerous practical applications in engineering and technology.

There are two special types of angular momentum:

1. Spin angular momentum: This is the angular momentum of an object about its own center of mass. For example, the Earth has a spin angular momentum due to its daily rotation around its polar axis.
2. Orbital angular momentum: This is the angular momentum of an object about a chosen center of rotation. For example, the Earth has an orbital angular momentum due to its revolution around the Sun.

The total angular momentum of an object is the sum of its spin and orbital angular momenta.

The conservation of angular momentum is an important principle in physics. According to this principle, the total angular momentum of a system remains constant unless acted upon by an external torque. This conservation law has various applications in different scientific disciplines, such as astronomy and quantum mechanics,

Formula for Angular Momentum

The formula for angular momentum is given by:

L = Iω

Where:

• L is the angular momentum
• I is the moment of inertia, which is a measure of an object's resistance to changes in its rotational motion
• ω is the angular velocity, which is the rate at which an object rotates around an axis.

The moment of inertia depends on the mass distribution of the object and how that mass is distributed relative to the axis of rotation. The angular velocity is the rate at which the object rotates, measured in radians per second.

Applications of Angular Momentum

Angular momentum has various applications in different fields of science and engineering. Some examples include:

• Astronomy: Angular momentum plays a crucial role in understanding the motion of celestial bodies. For example, the conservation of angular momentum explains why planets orbit the Sun in elliptical paths and why they maintain a relatively constant speed as they move closer or farther from the Sun.
• Quantum Mechanics: In quantum mechanics, angular momentum is quantized and is associated with the behavior of subatomic particles. The concept of angular momentum is used to describe the properties of electrons in atoms and the behavior of particles in quantum systems.
• Mechanical Engineering: Angular momentum is used in the design and analysis of rotating machinery, such as turbines, motors, and flywheels. Understanding angular momentum is crucial for optimizing the performance and stability of these systems

Overall, angular momentum is a fundamental concept that helps explain the rotational motion of objects and has wide-ranging applications in various scientific and engineering disciplines.