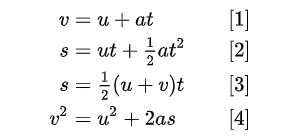
IB physics - Basics of kinematics , Important definitions and formula
"IB Physics Kinematics: Unveiling the Secrets of Motion in IB Physics"
Name: Own Teacher
Email: info@ownteacher.com
Created At: 03-09-2023
here is a more brief explanation of the kinematics terms and the equations for uniformly accelerated motion:
- Displacement: The distance moved in a particular direction. It is a vector quantity, which means it has both magnitude and direction. The SI unit for displacement is the meter (m).
- Velocity: The rate of change of displacement. It is a vector quantity that tells you how fast and in what direction an object is moving. The SI unit for velocity is meters per second (m/s).
- Speed: The magnitude of velocity. It tells you how fast an object is moving, but it does not tell you the direction of motion. The SI unit for speed is meters per second (m/s).
- Acceleration: The rate of change of velocity. It is a vector quantity that tells you how fast the velocity of an object is changing. The SI unit for acceleration is meters per second squared (m/s^2).
- Time: The duration of an event. The SI unit for time is the second (s).
8. **Scalar:** A scalar quantity is a physical quantity that has magnitude (size) but no direction. Speed is an example of a scalar quantity.
9. **Vector:** A vector quantity is a physical quantity that has both magnitude and direction. Displacement and velocity are examples of vector quantities.
10. **Uniform Motion:** Uniform motion occurs when an object moves with a constant speed in a straight line, resulting in a constant velocity and zero acceleration.
11. **Non-Uniform Motion:** Non-uniform motion occurs when an object's speed, direction, or both change over time, resulting in varying velocity and possible acceleration.
These definitions form the foundation for understanding and solving problems related to kinematics in AP Physics.
Certainly, here are the mathematical formulas for some of the relevant terms in kinematics:
1. **Displacement (Δx):**
Δx = x - x₀
where Δx is the displacement, x is the final position, and x₀ is the initial position.
2. **Velocity (v):**
v = Δx / Δt
where v is the velocity, Δx is the displacement, and Δt is the change in time.
3. **Speed (s):**
s = Δx / Δt
where s is the speed, Δx is the total distance traveled, and Δt is the total time taken.
4. **Acceleration (a):**
a = Δv / Δt
where a is the acceleration, Δv is the change in velocity, and Δt is the change in time.
These formulas are fundamental in solving problems related to kinematics, helping to calculate various motion parameters such as velocity, acceleration, and displacement.
Uniformly accelerated motion refers to the motion of an object in which the acceleration remains constant over time. In this type of motion, an object's velocity changes at a steady rate. It is a fundamental concept in classical mechanics and is often used to describe the motion of objects under the influence of gravity near the surface of the Earth.
Here are the key formulas associated with uniformly accelerated motion:
1. **Displacement (Δx):**
Δx = v₀t + (1/2)at²
where Δx is the displacement, v₀ is the initial velocity, t is the time, and a is the constant acceleration.
2. **Final Velocity (v):**
v = v₀ + at
where v is the final velocity, v₀ is the initial velocity, t is the time, and a is the constant acceleration.
3. **Velocity Squared (v²):**
v² = v₀² + 2aΔx
where v² is the final velocity squared, v₀ is the initial velocity, a is the constant acceleration, and Δx is the displacement.
where a is the acceleration, v is the final velocity, v₀ is the initial velocity, and t is the time.
These formulas allow you to calculate various parameters of an object's motion when it is undergoing uniformly accelerated motion, making it possible to analyze and predict its behavior under the influence of a constant force or acceleration.
Comment List
Leave a Comment.



