The Law of Conservation of Mechanical Energy is a fundamental principle in physics that states that the total mechanical energy of a closed system remains constant, provided there are no external forces doing work on the system. Here's a detailed explanation:

Mechanical Energy Components:

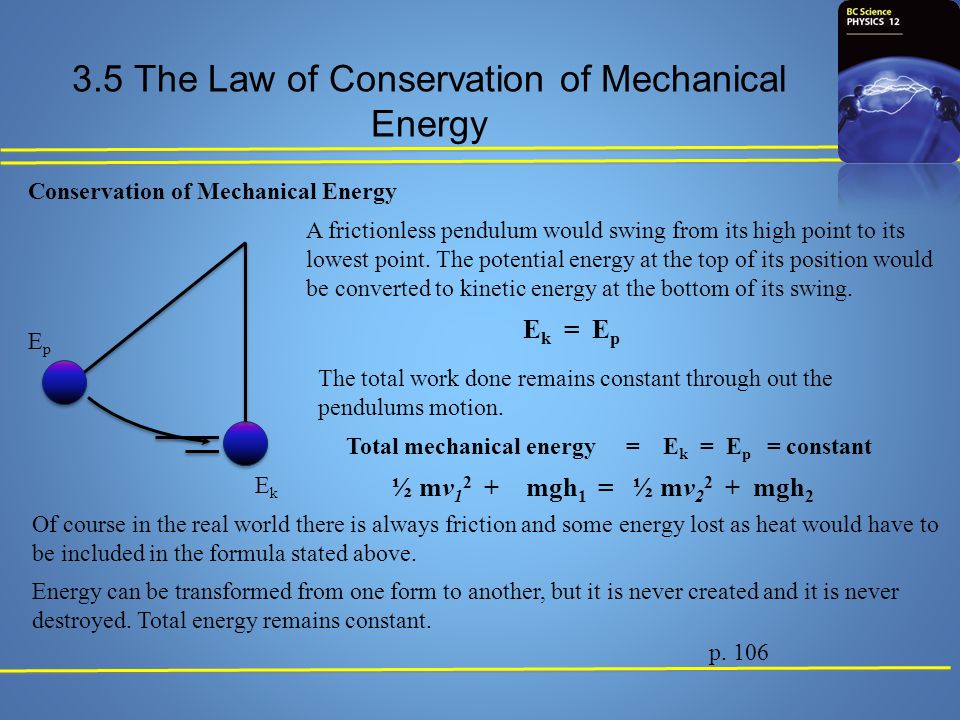
Kinetic Energy (KE): The energy associated with an object's motion. KE = (1/2) * m * v^2, where "m" is the mass of the object, and "v" is its velocity.

Potential Energy (PE): The energy associated with an object's position in a force field, such as gravitational potential energy (PE_gravity) or elastic potential energy (PE_elastic).

Conservation Principle:

• When no external forces (like friction, air resistance, or non-conservative forces) are acting on the system, the sum of kinetic energy and potential energy remains constant. In mathematical terms, KE_initial + PE_initial = KE_final + PE_final.

Applications:

Pendulum: As a pendulum swings back and forth, it converts potential energy to kinetic energy and back, with the total mechanical energy remaining constant.

Orbiting Objects: Celestial bodies in orbit, like planets around the Sun, follow elliptical paths while conserving their mechanical energy.

Spring-Mass System: In a spring-mass system, energy shifts between kinetic and elastic potential energy while obeying the conservation principle.

Significance:

• The Law of Conservation of Mechanical Energy simplifies the analysis of mechanical systems. It helps predict the behavior of objects, especially in the absence of dissipative forces.

Exceptions:

• In real-world scenarios, energy losses due to friction and air resistance can cause a deviation from perfect conservation. These losses are typically addressed using non-conservative work terms.

In summary, the Law of Conservation of Mechanical Energy is a powerful concept that states that the total mechanical energy of a closed system is constant when no external forces are doing work on it. This principle is a fundamental tool for understanding and predicting the behavior of objects in various physical systems.